Dynamic Time Warping

In this blog I want to talk about a similarity measures which is very useful for comparing time series data.
This is Dynamic Time Warping (DTW) [1] Let’s explore what it is.

Why do we need it?

First of all, as always, let’s try to understand why we even need a new fancy similarity measure like DTW.
The reason is that while simple similarity measures might fail for temporal sequences that differ in speed from each other, DTW shines.

For example:

For example: A = [0,1,0,1,0,1,0,1,0,1,0,1] B = [0,0,1,1,0,0,1,1,0,0,1,1]

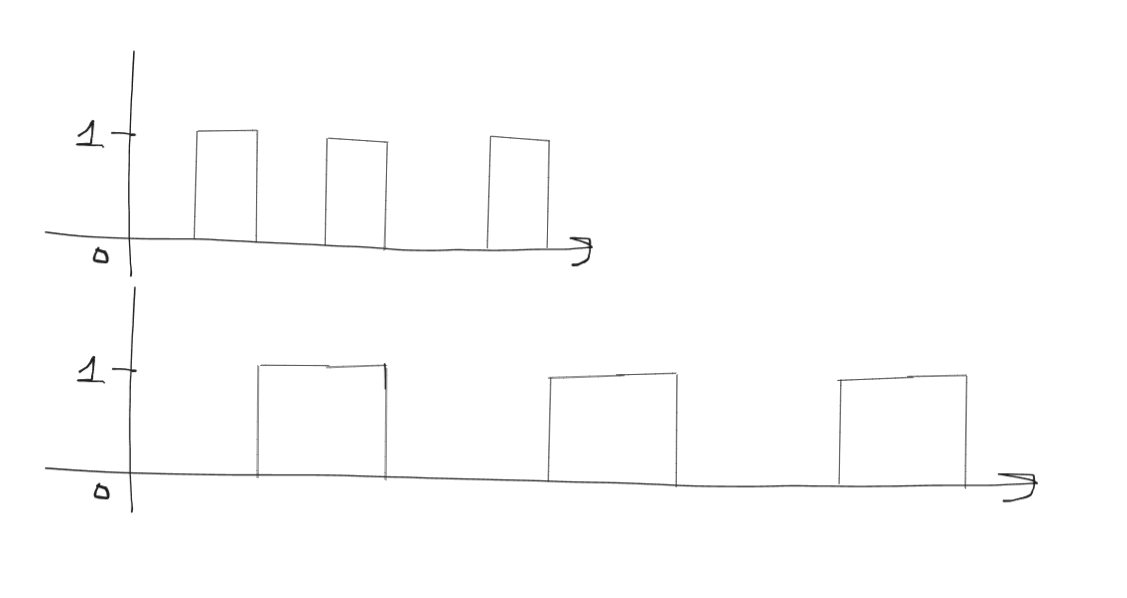
You can observe that these two signals have
Euclidean distance = 7, but if we calculate the DTW distance (will be covered later :D) it will be zero!

This might seem surprising at first but if you carefully observe the two signals it makes sense since they are quite similar.

We can see that A is just a sped up version of signal B.
\(\text{Timeperiod of B} = 2 \times \text{Timeperiod of A}\)

Another example comparing DTW and Eucledian Distance as a similarity measure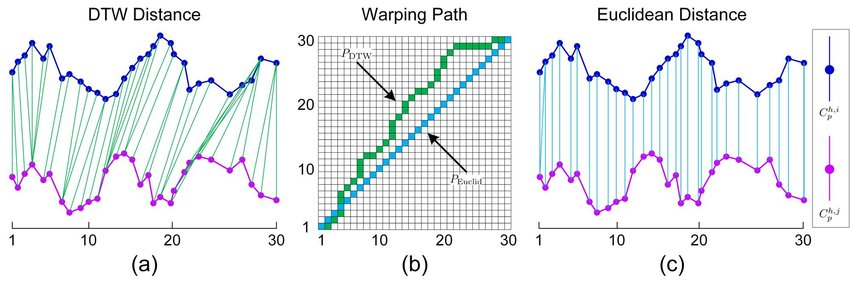

Formal Definition

Now that we have gotten some intuition about DTW, let’s look at the mathematical definition of DTW.

Let $ x $ and $ y $ be two time series of varying lengths such that
$ x \in \mathbb{R}^{n \times d} $ and $ y \in \mathbb{R}^{m \times d} $ or

\[x = \{ x_1, x_2, \dots, x_n \}, \quad y = \{ y_1, y_2, \dots, y_m \}\]

where $ x_i $ and $ y_i $ are $ d $-dimensional vectors.

Then,

\[DTW(x, y) = \min_{\pi} \sqrt{\sum_{(i,j) \in \pi} d(x_i, y_j)^2}\]

where $\pi = [\pi_0, \dots, \pi_K]$ is a path that satisfies the following properties:

• It is a list of index pairs $ \pi_k = (i_k, j_k) $ with $ 0 \leq i_k < n $ and $ 0 \leq j_k < m $.
• $ \pi_0 = (0, 0) $ and $ \pi_K = (n-1, m-1) $.
• For all $ k > 0 $, $ \pi_k = (i_k, j_k) $ is related to $ \pi_{k-1} = (i_{k-1}, j_{k-1}) $ as follows:
  • $ i_{k-1} \leq i_k \leq i_{k-1} + 1 $
  • $ j_{k-1} \leq j_k \leq j_{k-1} + 1 $

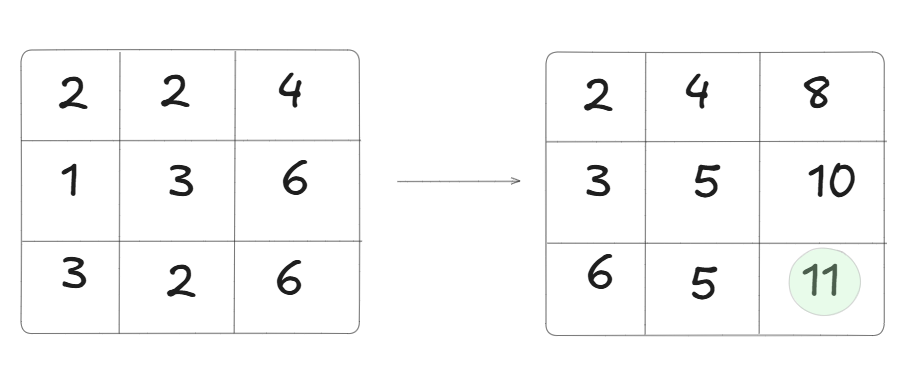
Let’s simplify this: what all this means is that first we construct an $ n \times m $ grid/matrix, say $ M $, where $ M_{i,j} $ denotes the Euclidean distance between $ x_i $ and $ y_j $.

After this we find the cumulative distances using dynamic programming. The idea is to find the shortest alignment path between the top left point $ M_{0,0} $ and the bottom right point $ M_{n-1, m-1} $. This means that we can only move in the directions $ (i+1, j) $, $ (i, j+1) $, or $ (i+1, j+1) $.
This can be achieved using DP in $ O(n^2) $ time complexity.

If you are unfamiliar with DP, don’t worry – it will get clear.
In a grid, how do you find the shortest alignment path between the top left and the bottom right point?
The idea is to use a greedy strategy where you keep track of the cumulative sum until the current point $ M_{i,j} $ and check the minimum increment in distance when you go to $ (M_{i+1,j}, M_{i,j+1}, M_{i+1,j+1}) $.
Since $ M_{i,j} \geq 0 $ for all $ i, j $, this will work.

Note: We are finding the shortes alignment path not the shortest path

Now, DP just provides us a way to cache the cumulative sum so that we don’t have to start from the base case every time for a point $ M_{i,j} $.

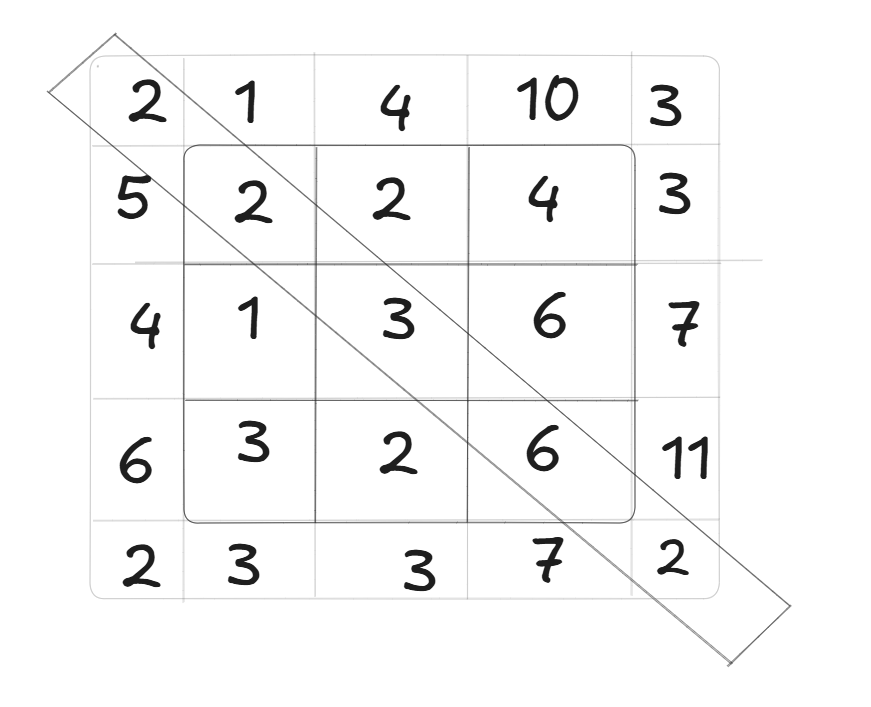
Basically,

\[DP(i,j,M) = M_{i,j} + \min\{DP(i-1,j), \; DP(i,j-1), \; DP(i-1,j-1)\}\]

On the left, the $ M $ matrix is shown, and on the right the DP matrix is shown.

The 11 circled in green in the right matrix is the shortest alignment distance(DTW distance) between $ M_{0,0} $ and $ M_{n-1, m-1} $.

Efficient DTW

$ O(nm) $ might be a problem if the time series is huge. For such cases there are 2 techniques that can help make the search for the shortest alignment path easier.

Sakoe Chiba Band

Instead of searching in the entire grid, we can create a bounding mask, i.e., restrict the search space. One of the techniques to do this is the Sakoe Chiba band [3].
Imagine placing a tube along the diagonal. This is exactly what the Sakoe Chiba band is. Now the width of this tube can be controlled by a parameter, say window.

If window = 0.1 then that means at each time step $ i $, the alignment can only shift within ±10% of the total sequence length. That means for $ DTW(i, j) $, the value of $ j $ must be within: \(i - 10 \leq j \leq i + 10\)

Itakura Max Slope

This controls how slanted the tube is. For example, if you want the search space to be something like this:

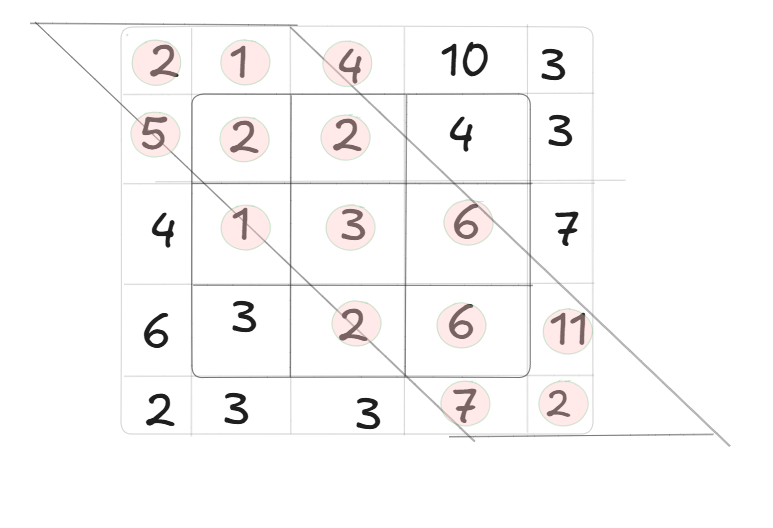
Note: There can be other kinds of bounding boxes; you can even create your own bounding box mask as well. Sakoe Chiba band is just an example which is widely used.

Optimal Alignment Path

After the DP matrix has been calculated, we can then backtrack in linear time $ O(n + m) $ because in each step, we move either:

• Diagonally $(i-1, j-1)$,
• Up $(i-1, j)$, or
• Left $(i, j-1)$, based on the minimum cost direction.

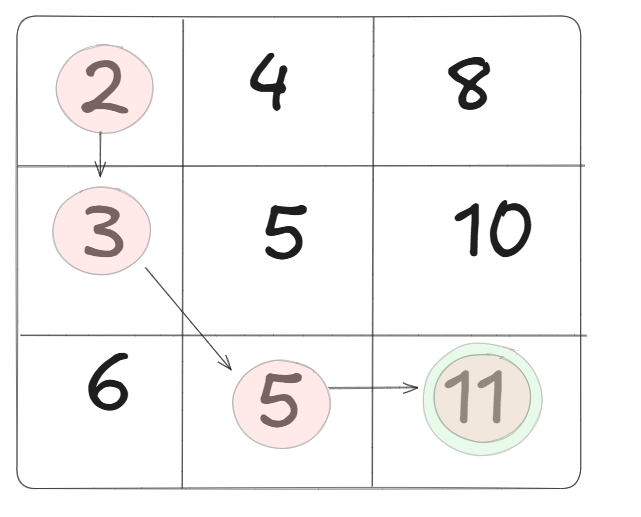
Example of Optimal Alignment Path

Note:
Dynamic Time Warping holds the following properties:

• $ \forall x, y, \; DTW(x, y) \geq 0 $
• $ \forall x, \; DTW(x, x) = 0 $

However, mathematically speaking, DTW is not a valid distance since it does not satisfy the triangular inequality.

---

References

1. [1] Dynamic Time Warping (DTW) Overview
2. [2] T. Vayer, R. Tavenard, L. Chapel, N. Courty, R. Flamary, and Y. Soullard, “Time Series Alignment with Global Invariances,” arXiv.org, 2020. https://arxiv.org/abs/2002.03848 (accessed Feb. 23, 2025).

3. [3] H. Sakoe and S. Chiba, “Dynamic programming algorithm optimization for spoken word recognition,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 26, no. 1, pp. 43–49, Feb. 1978, doi: https://doi.org/10.1109/tassp.1978.1163055.

4. Romain Tavenard, “DTW with Global Invariances,” Github.io, Dec. 17, 2020. https://rtavenar.github.io/hdr/parts/01/dtw/dtw_gi.html (accessed Feb. 23, 2025).
5. “dtw_distance,” aeon, 2025. https://www.aeon-toolkit.org/en/v1.0.0/api_reference/auto_generated/aeon.distances.dtw_distance.html (accessed Feb. 23, 2025).
6. “Dynamic Time Warping — tslearn 0.5.2 documentation,” tslearn.readthedocs.io. https://tslearn.readthedocs.io/en/stable/user_guide/dtw.html
7. Y. Li, R. W. Liu, Z. Liu, and J. Liu, “Similarity Grouping-Guided Neural Network Modeling for Maritime Time Series Prediction,” May 13, 2019. https://www.researchgate.net/publication/333077403_Similarity_Grouping-Guided_Neural_Network_Modeling_for_Maritime_Time_Series_Prediction

‌

‌

‌