Single Linkage Agglomerative Clustering |

The goal of this blog post is to understand how the Single Linkage Agglomerative Clustering works. To understand this, lets start with something more fundamental. What is Clustering?

Clustering

Lets start with a fun analogy to understand clustering and then formalize it. Lets say you have a basket of chips, unfortunately for you the chips of all the different flavors are mixed together. Being the perfectionist you are, you want to “cluster” them according to their flavor. To ease your task you have been given access to the “CHIPS-CLASSIFICATOR-9281RX” by the generous folks at IIT Gandhinagar, you can place the chips in it and it looks at the features of each chip and analyzes its “features” and pumps out an output label telling you what kind of chip flavor it is.

An image of the chips analogy

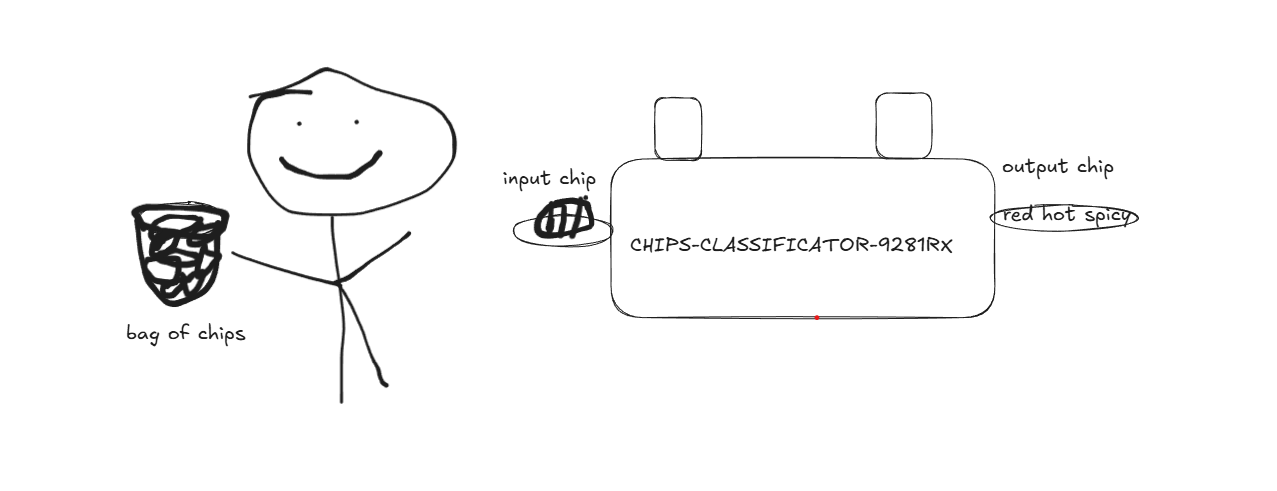
More formally, in machine learning Clustering is an unsupervised problem where given the “input data” we have to partition it according to the “features” of the data. This can also be said in another way Clustering is the task of grouping data in such a way that data points in the same cluster are more similar (this similarity metric is decided by you, an example is the euclidean distance) to each other than to those in other clusters.

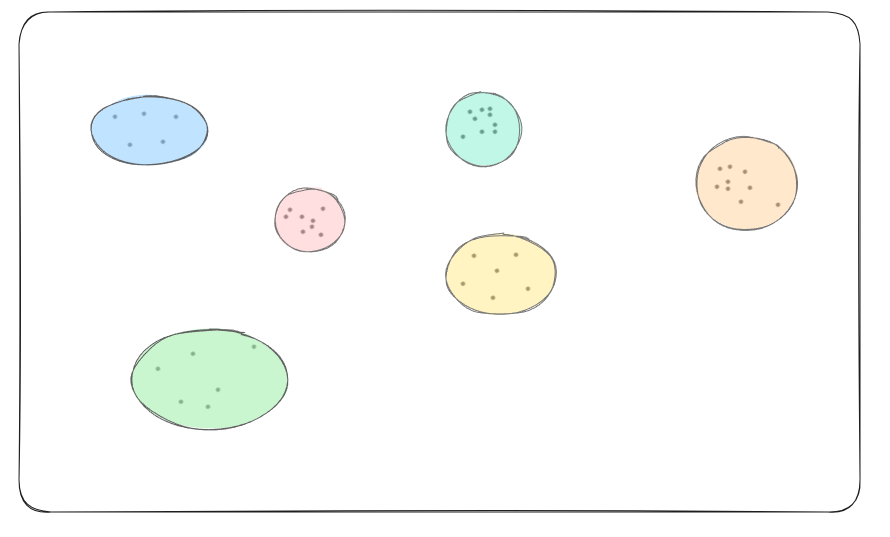
An example of clustering(6 clusters) based on euclidean distances

Single Linkage Agglomerative Custering

Great now that you know what clustering is(or maybe you already did), lets start with what the title promised, Single Linkage Agglomerative Clustering.

The main idea is to “keep merging closest set of data points, building larger clusters out of smaller ones”, this way we end up with a lot of different clusterings. If you know what hiererchical clustering, Single Linkage Clustering is a kind of hiererchical clustering.

Algo:
    Keep a current list of clusters
    Initially, each point in its own cluster
    while #clusters > 1:
          choose closest pair
          merge them,
          update list by deleting these and adding new cluster

Why bother with this?

Why do we need yet another algorithm if we already have kmeans? To answer that question lets look at the following example:

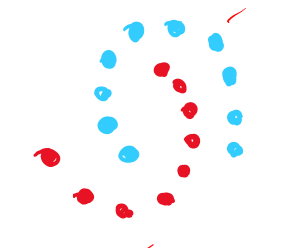
Example where k means struggles

For data like this where the idea clustering dosent necesssarily have “balls in high dim” algorithms like k means, k median struggle. In this case Single linkage clustering is easily able to cluster the data. This is because it dosent assume that the data will be distributed around the center of the cluster(ball shape). Instead, since it merges the clusters that are closer to each other first, it can adapt to a wider range of shapes of data.

Another reason why this algorithm might be useful is when we dont know the target number of clusters(hierechichal clusters are especially useful in this case), we can create a family of clusters for each k

How to define closeness of two clusters?

There are several ways to define closeness between two clusters. For example,

\[\begin{aligned} &\text{closest pair: single linkage clustering} \quad d_1(C, C') = \min_{x \in C, y \in C'} d(x, y) \\ &\text{Furthest pair: complete link clustering} \quad d_2(C, C') = \max_{x \in C, y \in C'} d(x, y) \\ &\text{Average of all pairs: average link} \quad d_3(C, C') = \text{avg}_{x \in C, y \in C'} d(x, y) \end{aligned}\]

Dendograph of hierechical clustering

Cost of Single Linkage Clustering

Single Linkage Clustering essentially creates clusters ${C_1, C_2,…, C_k}$ from the data that maximizes the minimum inter-cluster distance maximize ${Cost_k(C)}$ 𝑐𝑜𝑠𝑡_𝑘 (𝐶) = $\min d_{C_i, C_j}(C_i, C_j)$

Basically, assume among all the clusters the minimum distance between any 2 clusters is “d_min”, then it tries to maximize this.

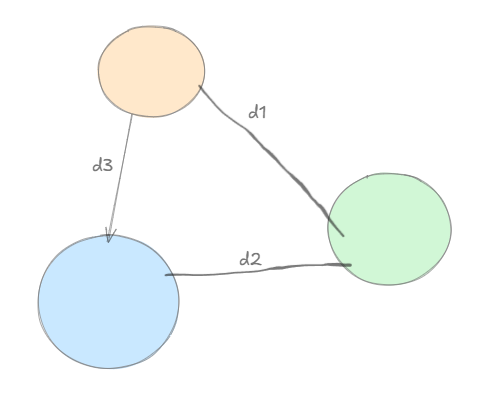
To illustrate the cost

As shown in the what the Single Linkage cost, tries to do is, maximize the cost where, cost = min(d1,d2,d3)

Properties of Single Linkage Clustering

Effective in low dimension but might struggle in higher dimension due to “curse of dimensionality”
Usually needs $O(n^2)$ space

Examples where Single Linkage might fail

TODO

Single Linkage Agglomerative Clustering